Up to now, you’ve used tools such as frequency tables, descriptive statistics, and scatter plots to describe and summarize the properties of your data. Now you’ll learn about probability, which provides the foundation for understanding and interpreting these statistics. You’ll also be introduced to statistical inference, which uses summary statistics to help you reach conclusions about your data.
Probability
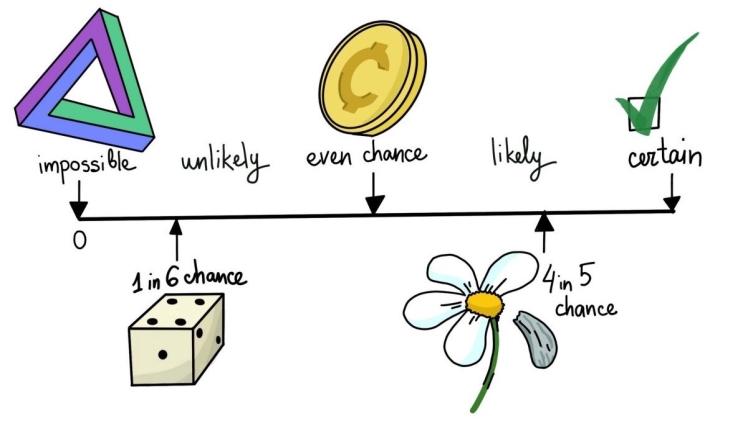
Much of science and mathematics is concerned with prediction. Some of these predictions can be made with great precision. Drop an object, and the laws of physics can predict how long the object will take to fall. Mix two chemicals, and the laws of chemistry can predict the properties of the resulting mixture. Other predictions can be made only in a general way.
Flip a coin, and you can predict that either a head or a tail will result, but you cannot predict which one. That doesn’t mean that you can’t say anything. If you flip the coin many times, you’ll notice that roughly half the flips result in heads and half result in tails. Flipping a coin is an example of a random phenomenon, in which individual outcomes are uncertain but follow a general pattern of occurrences.
This is difficult to do, and subtle biases can creep into even the most carefully designed studies. By observing the distribution of values in a random sample, we can draw some conclusions about the underlying probability distribution. As the sample size increases, the distribution of the values should more closely approximate the probability distribution. To return to our example of the shooter, by observing the spread of shots around the bull’s eye, we can estimate the probability distribution related to the shooter’s ability to hit the target. You can visit here to know medianewsfire.com.
Conclusion
Although many of the shots are near the bull’s eye, about a third of them are farther than 0.4 fitness at home horizontal unit away, either to the left or to the right of the target. Because these are random data, your values may be different. Based on the accuracy level you selected, a probability distribution showing the expected distribution of shots to the left or right of the target is also generated in the second column of the table.